Understanding Magnetic Induction

1. Magnetic Induction:

Magnetic induction is the process by which a magnetic field is formed in a substance or empty space due to changes in an external magnetic field. This can occur due to changes in electric current or changes in magnetic flux within a wire or ferromagnetic material. The primary laws governing magnetic induction are Faraday's Law and Lenz's Law.

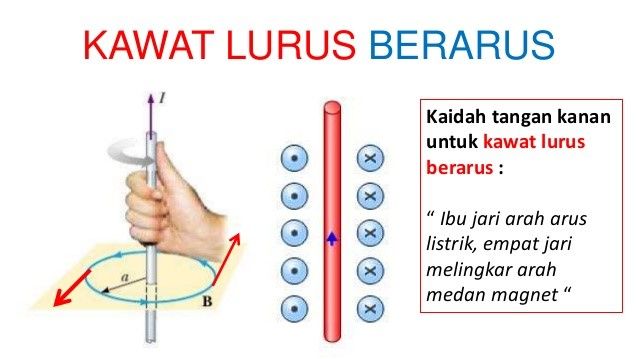
2. Magnetic Induction in Straight Current-Carrying Wire:

A straight current-carrying wire can create a magnetic field along its length. The strength of the magnetic field (\(B\)) at a specific distance from the wire with length (\(L\)) and current (\(I\)) can be calculated using the formula:

\(B = \frac{{\mu_0 \cdot I}}{{2\pi \cdot r}}\)

Where:

• \(B\) is the magnetic field strength (in tesla, T).
• \(\mu_0\) is the permeability of vacuum (approximately \(4\pi \times 10^{-7}\) Tm/A).
• \(I\) is the current magnitude (in amperes, A).
• \(r\) is the distance from the wire (in meters, m).

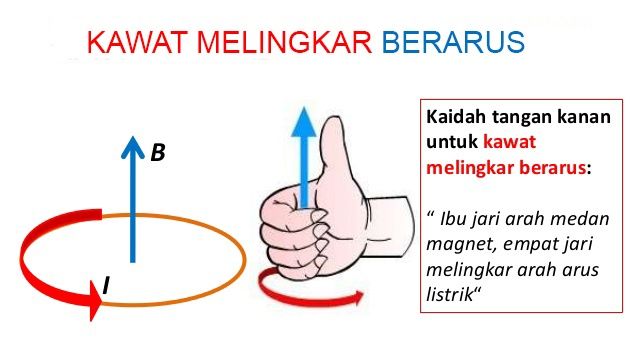
3. Magnetic Induction in Current Loop:

A current-carrying circular loop also generates a magnetic field around it. The strength of the magnetic field at the center of the loop with radius (\(r\)) and current (\(I\)) can be calculated using the formula:

\(B = \frac{{\mu_0 \cdot I}}{{2\pi \cdot r}}\)

This is similar to the formula for a straight wire because a circular loop can be considered as a collection of closely spaced straight wires forming a loop.

4. Magnetic Induction in Current-Carrying Solenoid:

A solenoid is a long coil of wire with an electric current running through it. The strength of the magnetic field inside the solenoid with length (\(L\)), number of turns (\(N\)), and current (\(I\)) can be calculated using the formula:

\(B = \mu_0 \cdot \frac{{N \cdot I}}{{L}}\)

Where:

• \(B\) is the magnetic field strength (in tesla, T).
• \(\mu_0\) is the permeability of vacuum (approximately \(4\pi \times 10^{-7}\) Tm/A).
• \(N\) is the number of turns in the solenoid.
• \(I\) is the current magnitude (in amperes, A).
• \(L\) is the length of the solenoid (in meters, m).

Magnetic Field at the End of the Solenoid:

The magnetic field at the end of a solenoid can be calculated using the formula:

\(B = \frac{{\mu_0 \cdot I \cdot N}}{{2 \cdot L}}\)

5. Magnetic Induction in Current-Carrying Toroid:

A toroid is a ring-shaped structure with a coiled wire around it. The strength of the magnetic field inside the toroid with the number of turns (\(N\)), current (\(I\)), and radius of the circle (\(r\)) can be calculated using the formula:

\(B = \frac{{\mu_0 \cdot N \cdot I}}{{2\pi \cdot r}}\)

This formula is also similar to the magnetic induction formula for a current loop because a toroid can be considered as a series of closely wound current loops forming a ring.